Question

Formatted question description: https://leetcode.ca/all/48.html

You are given an n x n 2D matrix representing an image, rotate the image by 90 degrees (clockwise).

You have to rotate the image in-place, which means you have to modify the input 2D matrix directly. DO NOT allocate another 2D matrix and do the rotation.

Example 1:

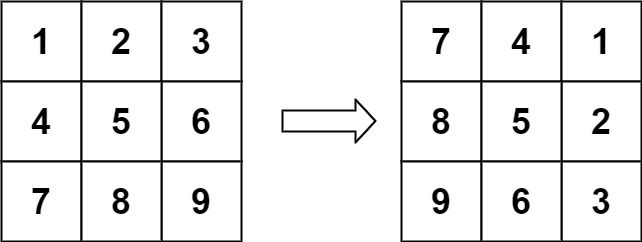
Input: matrix = [[1,2,3],[4,5,6],[7,8,9]]
Output: [[7,4,1],[8,5,2],[9,6,3]]

Example 2:

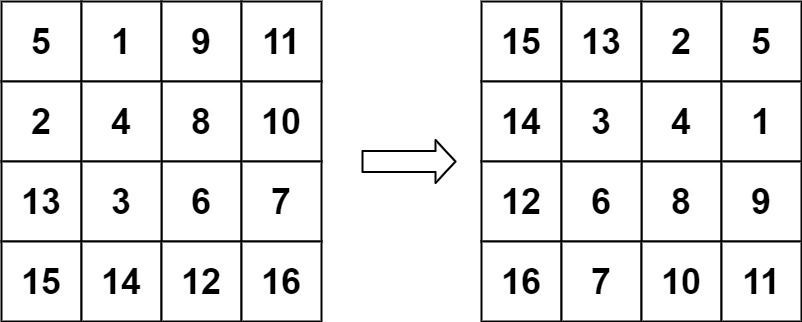
Input: matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
Output: [[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

Constraints:

n == matrix.length == matrix[i].length
1 <= n <= 20
-1000 <= matrix[i][j] <= 1000

Algorithm

Use a simple example to analyze:

2 3　　　 　　 7 4 1　

5 6　　-->　　 8 5 2　　

8 9 　　　 　　 9 6 3

There are many ways to flip 90 degrees, one or more steps can be solved, first look at a direct method, this method is to cover the previous numbers in a clockwise order, starting from the four top corners, and then To traverse in the middle, the coordinates covered each time are the same, as follows:

(i, j) <- (n-1-j, i) <- (n-1-i, n-1-j) <- (j, n-1-i)

This is actually a cyclic process. The first position covers the fourth position, where the value range of i is [0, n/2), and the value range of j is [i, n-1-i), As for why i and j are in this value range, why i don’t need to traverse [n/2, n). If you carefully observe the relationship between these positions, it is not difficult to find that the range of column j is actually [i, n-1 -i) Turn 90 degrees clockwise, which is exactly the position of [n/2, n) in row i. This method changes four numbers each time through the loop

Note

I missed a key concept, I DO NOT have to rotate all numbers on one edge from start to end

1. for corner positions of each layer, rotate first is also changing end of that layer row
2. for numbers not corner, rotate them


eg:
	1 2
	3 4

	one rotate is enough, since except corner position, no other positions


eg:
	1   2   3   4   5
	6   7   8   9   10
	11  12  13  14  15
	16  17  18  19  20
	21  22  23  24  25

	like in row "1,2,3,4,5", rotate 1 will also change 5
	so, for each edge, rotate to the penultimate one, that is, only rotate "1,2,3,4" is enough, and 5 will be processed in the next operation

another way: transpose + reflect

reference https://leetcode.com/problems/rotate-image/solution/

original

[
	[1,2,3],
	[4,5,6],
	[7,8,9]
]

diagonal as reverse base line

[
	[1,4,7],
	[2,5,8],
	[3,6,9]
]

every row, to reverse from left to right

[
	[7,4,1],
	[8,5,2],
	[9,6,3]
]

Code

public class Rotate_Image {

	public class Solution {
	    /*  eg:

	        1   2   3   4   5
	        6   7   8   9   10
	        11  12  13  14  15
	        16  17  18  19  20
	        21  22  23  24  25
	    */

	    public void rotate(int[][] m) { // m for matrix

	        if (m == null || m.length == 0) {
	            return;
	        }

	        // for each circle, start position is (i,i), length is rectangle size
	        // eg. above: (0,0), length=5; (1,1), length=3
	        int i = 0;
	        int length = m.length;

	        while (i < m.length / 2) {

	            int count = 0;
	            while (count < length - 1) { // @note: extra attention here "-1".
	            // while (count < length) {

	                int tmp = m[i][i + count];

	                // i+length-1: last index of this rectangle
	                // i+length-1 - count: index from backward
	                m[i][i + count] = m[i + length - 1 - count][i];
	                m[i + length - 1 - count][i] = m[i + length - 1][i + length - 1 - count];
	                m[i + length - 1][i + length - 1 - count] = m[i + count][i + length - 1];
	                m[i + count][i + length - 1] = tmp;

	                count++;
	            }

	            length -= 2; // @note: shrink each edge length by 2
	            i++; // start point moving along diagonal
	        }
	    }
	}

	// An Inplace function to rotate a N x N matrix by 90 degrees in anti-clockwise direction
	static void rotateMatrix_anticlock(int N, int mat[][])
	{
		// Consider all squares one by one
		for (int x = 0; x < N / 2; x++) {
			// Consider elements in group of 4 in
			// current square
			for (int y = x; y < N-x-1; y++) {
				// store current cell in temp variable
				int temp = mat[x][y];

				// move values from right to top
				mat[x][y] = mat[y][N-1-x];

				// move values from bottom to right
				mat[y][N-1-x] = mat[N-1-x][N-1-y];

				// move values from left to bottom
				mat[N-1-x][N-1-y] = mat[N-1-y][x];

				// assign temp to left
				mat[N-1-y][x] = temp;
			}
		}
	}

	static void rotateMatrix_clockwise(int N, int mat[][])
	{
		// Consider all squares one by one
		for (int x = 0; x < N / 2; x++) {
			// Consider elements in group of 4 in
			// current square
			for (int y = x; y < N-x-1; y++) {
				// store current cell in temp variable
				int temp = mat[x][y];

				// move values from right to top
				mat[x][y] = mat[y][N-1-x];

				// move values from bottom to right
				mat[y][N-1-x] = mat[N-1-x][N-1-y];

				// move values from left to bottom
				mat[N-1-x][N-1-y] = mat[N-1-y][x];

				// assign temp to left
				mat[N-1-y][x] = temp;
			}
		}
	}
}

//////

class Solution_diagonal {
	public void rotate(int[][] matrix) {
		transpose(matrix);
		reflect(matrix);
	}

	public void transpose(int[][] matrix) {
		int n = matrix.length;
		for (int i = 0; i < n; i++) {
			for (int j = i; j < n; j++) {
				int tmp = matrix[j][i];
				matrix[j][i] = matrix[i][j];
				matrix[i][j] = tmp;
			}
		}
	}

	public void reflect(int[][] matrix) {
		int n = matrix.length;
		for (int i = 0; i < n; i++) {
			for (int j = 0; j < n / 2; j++) {
				int tmp = matrix[i][j];
				matrix[i][j] = matrix[i][n - j - 1];
				matrix[i][n - j - 1] = tmp;
			}
		}
	}
}

//////

class Solution {
    public void rotate(int[][] matrix) {
        int s = 0, n = matrix.length;
        while (s < (n >> 1)) {
            int e = n - s - 1;
            for (int i = s; i < e; ++i) {
                int t = matrix[i][e];
                matrix[i][e] = matrix[s][i];
                matrix[s][i] = matrix[n - i - 1][s];
                matrix[n - i - 1][s] = matrix[e][n - i - 1];
                matrix[e][n - i - 1] = t;
            }
            ++s;
        }
    }
}

// OJ: https://leetcode.com/problems/rotate-image/
// Time: O(N^2)
// Space: O(1)
class Solution {
public:
    void rotate(vector<vector<int>>& A) {
        int N = A.size();
        for (int i = 0; i < N / 2; ++i) {
            for (int j = i; j < N - i - 1; ++j) {
                int tmp = A[i][j];
                A[i][j] = A[N - j - 1][i];
                A[N - j - 1][i] = A[N - i - 1][N - j - 1];
                A[N - i - 1][N - j - 1] = A[j][N - i - 1];
                A[j][N - i - 1] = tmp;
            }
        }
    }
};

class Solution(object):
  def rotate(self, matrix):
    """
    :type matrix: List[List[int]]
    :rtype: void Do not return anything, modify matrix in-place instead.
    """
    if len(matrix) == 0:
      return
    h = len(matrix)
    w = len(matrix[0])
    for i in range(0, h): # mirror
      for j in range(0, w / 2):
        matrix[i][j], matrix[i][w - j - 1] = matrix[i][w - j - 1], matrix[i][j]

    for i in range(0, h): # transpos
      for j in range(0, w - 1 - i):
        matrix[i][j], matrix[w - 1 - j][h - 1 - i] = matrix[w - 1 - j][h - 1 - i], matrix[i][j]


############

class Solution:
    def rotate(self, matrix: List[List[int]]) -> None:
        n = len(matrix)
        for i in range(n >> 1):
            for j in range(n):
                matrix[i][j], matrix[n - i - 1][j] = matrix[n - i - 1][j], matrix[i][j]
        for i in range(n):
            for j in range(i):
                matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]

func rotate(matrix [][]int) {
	n := len(matrix)
	// matrix transpose
	for i := 0; i < n; i++ {
		for j := i; j < n; j++ {
			matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]
		}
	}
	// reverse each matrix[i]
	for i := 0; i < n; i++ {
		for j, k := 0, n-1; j < k; j, k = j+1, k-1 {
			matrix[i][j], matrix[i][k] = matrix[i][k], matrix[i][j]
		}
	}
}

/**
 Do not return anything, modify matrix in-place instead.
 */
function rotate(matrix: number[][]): void {
    let n = matrix[0].length;
    for (let i = 0; i < Math.floor(n / 2); i++) {
        for (let j = 0; j < Math.floor((n + 1) / 2); j++) {
            let tmp = matrix[i][j];
            matrix[i][j] = matrix[n - 1 - j][i];
            matrix[n - 1 - j][i] = matrix[n - 1 - i][n - 1 - j];
            matrix[n - 1 - i][n - 1 - j] = matrix[j][n - 1 - i];
            matrix[j][n - 1 - i] = tmp;
        }
    }
}

/**
 * @param {number[][]} matrix
 * @return {void} Do not return anything, modify matrix in-place instead.
 */
var rotate = function (matrix) {
    matrix.reverse();
    for (let i = 0; i < matrix.length; i++) {
        for (let j = 0; j < i; j++) {
            [matrix[i][j], matrix[j][i]] = [matrix[j][i], matrix[i][j]];
        }
    }
};

impl Solution {
    pub fn rotate(matrix: &mut Vec<Vec<i32>>) {
        let n = matrix.len();
        for i in 0..n / 2 {
            for j in i..n - i - 1 {
                let t = matrix[i][j];
                matrix[i][j] = matrix[n - j - 1][i];
                matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1];
                matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1];
                matrix[j][n - i - 1] = t;
            }
        }
    }
}

public class Solution {
    public void Rotate(int[][] matrix) {
        int n = matrix.Length;
        for (int i = 0; i < n >> 1; ++i) {
            for (int j = 0; j < n; ++j) {
                int t = matrix[i][j];
                matrix[i][j] = matrix[n - i - 1][j];
                matrix[n - i - 1][j] = t;
            }
        }
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < i; ++j) {
                int t = matrix[i][j];
                matrix[i][j] = matrix[j][i];
                matrix[j][i] = t;
            }
        }
    }
}

48 - Rotate Image

Question

Algorithm

Note

another way: transpose + reflect

Code

All Problems

All Solutions

Welcome to Subscribe On Youtube

Question

Algorithm

Note

another way: transpose + reflect

Code

All Problems

All Solutions