Formatted question description: https://leetcode.ca/all/23.html

23 - Merge k Sorted Lists

Merge k sorted linked lists and return it as one sorted list. Analyze and describe its complexity.

Example:

Input: [ 1->4->5, 1->3->4, 2->6 ]

Output: 1->1->2->3->4->4->5->6

MergeSort solution

The initial approach one might consider is to merge the linked lists two at a time. That is, first merge the first two lists, then merge the result with the third list, and continue this process until the kth list. While this approach is theoretically sound, it proves to be inefficient for passing online judgment (OJ) systems due to its higher time complexity. Therefore, a shift in strategy is essential, leading us to adopt the Divide and Conquer method.

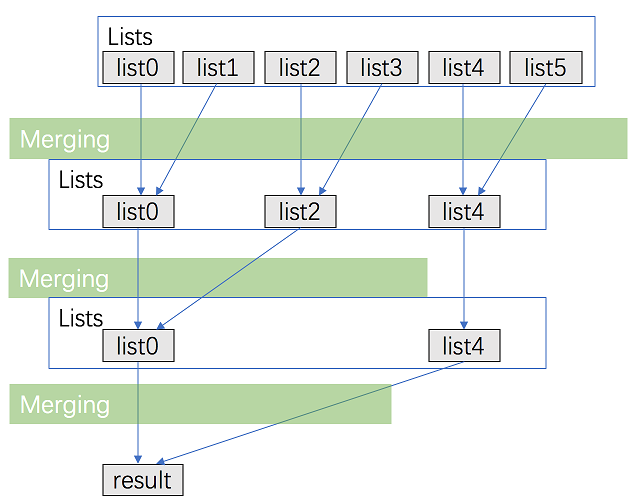
In essence, this method involves repeatedly dividing the task into smaller, more manageable chunks. Specifically, the k linked lists are initially divided into tasks of merging k/2 pairs of linked lists. This process continues recursively, dividing the lists until we are left with tasks that involve merging only one or two linked lists, at which point the actual merging begins.

Consider the task of merging 6 linked lists. Using the divide and conquer strategy, the first step would be to merge lists 0 and 3, 1 and 4, and 2 and 5, respectively. In the next iteration, you would only need to merge 3 linked lists, further merging lists 1 and 3, and finally merging this result with list 2.

The variable k in the code is determined using the formula (n+1)/2. The addition of 1 serves a specific purpose:

It ensures that when n is odd, k starts from the latter half of the list array. For instance, if n=5, then k=3. This setup leads to the merging of lists 0 and 3, and 1 and 4, leaving list 2 untouched initially.
When n is even, adding 1 has no effect. For example, with n=4, k=2 aligns perfectly for the merging process: lists 0 and 2 are merged, as are lists 1 and 3.

This adjustment elegantly addresses the challenge of merging an odd number of lists and demonstrates the efficiency of the Divide and Conquer approach in solving the problem of merging k linked lists.

big-o analysis

time-complex O(N*logK)

N is the total number of nodes

k is the number of linked lists.

      public ListNode merge(ListNode[] lists, int start, int end) {

          int mid = (end - start) / 2 + start;
          ListNode leftHalf = merge(lists, start, mid);
          ListNode rightHalf = merge(lists, mid + 1, end);

      }

Reference: https://leetcode.com/problems/merge-k-sorted-lists/solution/

We can merge two sorted linked list in O(n) time where n is the total number of nodes in two lists.
Sum up the merge process and we can get: sum all nodes logk times (height of tree) => O(Nlogk)

Heap-Based Solution

To efficiently merge k sorted linked lists, a heap-based solution leverages the properties of a priority queue, specifically a min heap. This approach involves the following steps:

Initialization: Place the smallest node (head node) from each of the k lists into a min heap. This ensures that the heap always contains the smallest available nodes from each list at any given time.
Process Nodes:
- Extract (poll) the smallest node from the heap.
- If the polled node has a successor (i.e., polled.next is not null) in its corresponding list, insert that successor node into the heap.
- Continue this process until the heap is empty, indicating that all nodes have been processed and merged into a single sorted list.

It’s important to note that the heap’s size is maintained at k, the number of lists, since we only insert the smallest node of each list into the heap initially and replace it with the next node from the same list as we poll nodes from the heap. The insertion operation has a complexity of O(log k), and since we insert a total of nk nodes (n being the average number of nodes in each list), the overall time complexity of this solution is O(n * k * log k).

Key Implementation Details

Heap Operations: We use heap.offer() to add new nodes to the heap. It’s crucial to check that the node to be offered is not null since the offer() method does not accept null values. This check is performed with if (polled.next != null) before calling heap.offer(polled.next).
Complexity Analysis:
- Time Complexity: The solution has a time complexity of O(n * k * log k) due to the log k complexity of heap insertions (offer) and nk total insertions.
- Space Complexity: The space complexity is O(k) because the heap size does not exceed k, the number of linked lists.

Example

Consider merging three linked lists with a total of n nodes. The smallest node from each list is initially added to the heap. When a node is polled from the heap, its successor (if any) is added to the heap. This process ensures that at every step, the heap helps us find the next smallest node to be added to the merged list.

Conclusion

The heap-based solution for merging k sorted linked lists is efficient and elegant, leveraging the min heap’s properties to ensure that the merged list is sorted with optimal time and space complexity. This method stands out for its ability to handle multiple lists simultaneously while maintaining a manageable heap size.

public class Merge_k_Sorted_Lists {

    public static void main(String[] args) {

        Merge_k_Sorted_Lists out = new Merge_k_Sorted_Lists();
        Solution s = out.new Solution();

        ListNode l1 = null;
        ListNode l2 = new ListNode(1);

        s.mergeKLists(new ListNode[]{l1, l2});

    }

    public class Solution {
        public ListNode mergeKLists(ListNode[] lists) {

            if (lists == null || lists.length == 0) {
                return null;
            }

            // same as merge sort array
            return merge(lists, 0, lists.length - 1);
        }

        public ListNode merge(ListNode[] lists, int start, int end) {

            // single list
            if (start == end) {
                return lists[start];
            }

            int mid = (end - start) / 2 + start;
            ListNode leftHalf = merge(lists, start, mid);
            ListNode rightHalf = merge(lists, mid + 1, end);

            return mergeTwoLists(leftHalf, rightHalf);
        }

        // from previous question: 21 Merge Two Sorted Lists
        public ListNode mergeTwoLists(ListNode l1, ListNode l2) {

            ListNode dummy = new ListNode(0);
            ListNode current = dummy;

            while (l1 != null || l2 != null) {
                int v1 = (l1 == null ? Integer.MAX_VALUE : l1.val);
                int v2 = (l2 == null ? Integer.MAX_VALUE : l2.val);

                if (v1 < v2) {
                    current.next = l1;
                    l1 = l1.next;
                } else {
                    current.next = l2;
                    l2 = l2.next;
                }

                current = current.next; // now current is the new end node, but still pointing to next node
                current.next = null; // @note: key, cut this node from l1 or l2
            }

            return dummy.next;
        }
    }

}

//////

class Solution_Heap {
	public ListNode mergeKLists(ListNode[] lists) {

		if (lists == null || lists.length == 0) {
			return null;
		}

		ListNode dummy = new ListNode(0);
		ListNode current = dummy;

		// put 1st of each list to heap
		PriorityQueue<ListNode> heap = new PriorityQueue<>(
			(a,b) -> a.val - b.val
		);

		//
		Arrays.stream(lists).filter(Objects::nonNull).forEach(heap::offer);

		while (heap.size() != 0) {
			ListNode polled = heap.poll();

			current.next = polled;
			current = current.next;

			if (polled.next != null) {
				heap.offer(polled.next); // @note: heap.offer()参数不能是null
			}
		}

		return dummy.next;
	}
}

//////

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode mergeKLists(ListNode[] lists) {
        int n = lists.length;
        if (n == 0) {
            return null;
        }
        for (int i = 0; i < n - 1; ++i) {
            lists[i + 1] = mergeLists(lists[i], lists[i + 1]);
        }
        return lists[n - 1];
    }

    private ListNode mergeLists(ListNode l1, ListNode l2) {
        ListNode dummy = new ListNode();
        ListNode cur = dummy;
        while (l1 != null && l2 != null) {
            if (l1.val <= l2.val) {
                cur.next = l1;
                l1 = l1.next;
            } else {
                cur.next = l2;
                l2 = l2.next;
            }
            cur = cur.next;
        }
        cur.next = l1 == null ? l2 : l1;
        return dummy.next;
    }
}

// OJ: https://leetcode.com/problems/merge-k-sorted-lists/
// Time: O(NlogK)
// Space: O(K)
class Solution {
public:
    ListNode* mergeKLists(vector<ListNode*>& lists) {
        ListNode dummy, *tail = &dummy;
        auto cmp = [](auto a, auto b) { return a->val > b->val; };
        priority_queue<ListNode*, vector<ListNode*>, decltype(cmp)> q(cmp);
        for (auto list : lists) {
            if (list) q.push(list); // avoid pushing NULL list.
        }
        while (q.size()) {
            auto node = q.top();
            q.pop();
            if (node->next) q.push(node->next);
            tail->next = node;
            tail = node;
        }
        return dummy.next;
    }
};

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution:
    def mergeKLists(self, lists: List[Optional[ListNode]]) -> Optional[ListNode]:
        setattr(ListNode, "__lt__", lambda a, b: a.val < b.val)
        pq = [head for head in lists if head]
        heapify(pq)
        dummy = cur = ListNode()
        while pq:
            node = heappop(pq)
            if node.next:
                heappush(pq, node.next)
            cur.next = node
            cur = cur.next
        return dummy.next


# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next

######


import heapq


'''
__lt__(self, other) for <
__le__(self,other) for <=
__gt__(self, other) for >
__ge__(self, other) for >=
'''

'''
# or create a wrapper class, without modifying existing node class
class NodeWrapper:
    def __init__(self, node):
        self.node = node
    
    def __lt__(self, other):
        return self.node.val < other.node.val

'''

# overwrite the comparison function, so the node can be comparable
# or else, error, TypeError: '<' not supported between instances of 'ListNode' and 'ListNode'

# define 'gt' will also work, so either lt or gt will do the compare job for ListNode
# ListNode.__gt__ = lambda x, y: (x.val > y.val)

ListNode.__lt__ = lambda x, y: (x.val < y.val)

class Solution:

    def mergeKLists(self, lists: List[Optional[ListNode]]) -> Optional[ListNode]:
        dummy = current = ListNode()
        heap = []
        for i, node in enumerate(lists):
            if node:
                # need to override
                # or else error: TypeError: '<' not supported between instances of 'ListNode' and 'ListNode'
                heapq.heappush(heap, node)

        while heap:
            anode = heapq.heappop(heap)

            current.next = anode
            current = current.next

            if anode.next:
                heapq.heappush(heap, anode.next)

        return dummy.next

'''
tried to use node.val to order heap, but still got error TypeError: '<' not supported between instances of 'ListNode' and 'ListNode': 

heapq.heappush(heap, (node.val, node))

'''

######

# based on merge 2 lists
# note for empty input
class Solution:
    def mergeKLists(self, lists: List[Optional[ListNode]]) -> Optional[ListNode]:
        if lists is None or len(lists) == 0:
            return None
        return self.mergeKListsHelper(lists, 0, len(lists) - 1)

    def mergeKListsHelper(self, lists: List[Optional[ListNode]], start: int, end: int) -> Optional[ListNode]:

        if start == end:
            return lists[start]

        mid = int((start + end) / 2)

        left = self.mergeKListsHelper(lists, start, mid)
        # print(left)

        right = self.mergeKListsHelper(lists, mid + 1, end)
        # print(right)

        return self.mergeTwoLists(left, right)

    def mergeTwoLists(self, list1: Optional[ListNode], list2: Optional[ListNode]) -> Optional[ListNode]:
        dummy = ListNode()
        current = dummy
        # print("merging: ", list1)
        # print("merging: ", list2)
        while list1 or list2:
            v1 = list1.val if list1 else float('inf')
            v2 = list2.val if list2 else float('inf')

            if v1 < v2:
                current.next = list1
                list1 = list1.next
            else:
                current.next = list2
                list2 = list2.next
            current = current.next

        # print("merging result: ", dummy.next)

        return dummy.next

############

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution:
    def mergeKLists(self, lists: List[ListNode]) -> ListNode:
        n = len(lists)
        if n == 0:
            return None
        for i in range(n - 1): # this is o(N) times of merge, while if use divide-mid-mere then it's o(logN) times of merge
            lists[i + 1] = self.mergeTwoLists(lists[i], lists[i + 1])
        return lists[-1]

    def mergeTwoLists(self, l1: ListNode, l2: ListNode) -> ListNode:
        dummy = ListNode()
        cur = dummy
        while l1 and l2:
            if l1.val <= l2.val:
                cur.next = l1
                l1 = l1.next
            else:
                cur.next = l2
                l2 = l2.next
            cur = cur.next
        cur.next = l1 or l2
        return dummy.next



if __name__ == '__main__':

    l1 = ListNode(1)
    l1.next = ListNode(4)
    l1.next.next = ListNode(5)

    l2 = ListNode(1)
    l2.next = ListNode(3)
    l2.next.next = ListNode(4)

    l3 = ListNode(2)
    l3.next = ListNode(6)

    print(Solution().mergeKLists([l1, l2, l3]))

    print(Solution().mergeKLists([]))
    print(Solution().mergeKLists([[]]))

/**
 * Definition for singly-linked list.
 * type ListNode struct {
 *     Val int
 *     Next *ListNode
 * }
 */
 func mergeKLists(lists []*ListNode) *ListNode {
    n := len(lists)
    if n == 0 {
        return nil
    }
    for i := 1; i < n; i++ {
        lists[i] = mergeTwoLists(lists[i-1], lists[i])
    }
    return lists[n-1]
}

 func mergeTwoLists(l1 *ListNode, l2 *ListNode) *ListNode {
    dummy := &ListNode{}
    cur := dummy
    for l1 != nil && l2 != nil {
        if l1.Val <= l2.Val {
            cur.Next = l1
            l1 = l1.Next
        } else {
            cur.Next = l2
            l2 = l2.Next
        }
        cur = cur.Next
    }
    if l1 != nil {
        cur.Next = l1
    } else if l2 != nil {
        cur.Next = l2
    }
    return dummy.Next
}

/**
 * Definition for singly-linked list.
 * class ListNode {
 *     val: number
 *     next: ListNode | null
 *     constructor(val?: number, next?: ListNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.next = (next===undefined ? null : next)
 *     }
 * }
 */

function mergeKLists(lists: Array<ListNode | null>): ListNode | null {
    const n = lists.length;
    const dfs = (start: number, end: number) => {
        if (end - start <= 1) {
            return lists[start] ?? null;
        }

        const mid = (start + end) >> 1;
        let left = dfs(start, mid);
        let right = dfs(mid, end);

        const dummy = new ListNode();
        let cur = dummy;
        while (left || right) {
            let next: ListNode;
            if (
                (left ?? { val: Infinity }).val <
                (right ?? { val: Infinity }).val
            ) {
                next = left;
                left = left.next;
            } else {
                next = right;
                right = right.next;
            }
            cur.next = next;
            cur = next;
        }
        return dummy.next;
    };
    return dfs(0, n);
}

/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */
/**
 * @param {ListNode[]} lists
 * @return {ListNode}
 */
var mergeKLists = function (lists) {
    const n = lists.length;
    if (n == 0) {
        return null;
    }
    for (let i = 1; i < n; ++i) {
        lists[i] = mergeTwoLists(lists[i - 1], lists[i]);
    }
    return lists[n - 1];
};

function mergeTwoLists(l1, l2) {
    const dummy = new ListNode();
    let cur = dummy;
    while (l1 && l2) {
        if (l1.val <= l2.val) {
            cur.next = l1;
            l1 = l1.next;
        } else {
            cur.next = l2;
            l2 = l2.next;
        }
        cur = cur.next;
    }
    cur.next = l1 || l2;
    return dummy.next;
}

# Definition for singly-linked list.
# class ListNode
#     attr_accessor :val, :next
#     def initialize(val = 0, _next = nil)
#         @val = val
#         @next = _next
#     end
# end
# @param {ListNode[]} lists
# @return {ListNode}
def merge_k_lists(lists)
  n = lists.length
  i = 1
  while i < n
      lists[i] = merge_two_lists(lists[i - 1], lists[i])
      i += 1
  end
  lists[n - 1]
end

def merge_two_lists(l1, l2)
dummy = ListNode.new()
cur = dummy
while l1 && l2
    if l1.val <= l2.val
        cur.next = l1
        l1 = l1.next
    else
        cur.next = l2
        l2 = l2.next
    end
    cur = cur.next
end
cur.next = l1 || l2
dummy.next
end

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     public int val;
 *     public ListNode next;
 *     public ListNode(int val=0, ListNode next=null) {
 *         this.val = val;
 *         this.next = next;
 *     }
 * }
 */
public class Solution {
    public ListNode MergeKLists(ListNode[] lists) {
        int n = lists.Length;
        if (n == 0) {
            return null;
        }
        for (int i = 1; i < n; ++i) {
            lists[i] = MergeTwoLists(lists[i - 1], lists[i]);
        }
        return lists[n - 1];
    }

    private ListNode MergeTwoLists(ListNode l1, ListNode l2) {
        ListNode dummy = new ListNode();
        ListNode cur = dummy;
        while (l1 != null && l2 != null) {
            if (l1.val <= l2.val) {
                cur.next = l1;
                l1 = l1.next;
            } else {
                cur.next = l2;
                l2 = l2.next;
            }
            cur = cur.next;
        }
        cur.next = l1 == null ? l2 : l1;
        return dummy.next;
    }
}

// Definition for singly-linked list.
// #[derive(PartialEq, Eq, Clone, Debug)]
// pub struct ListNode {
//   pub val: i32,
//   pub next: Option<Box<ListNode>>
// }
//
// impl ListNode {
//   #[inline]
//   fn new(val: i32) -> Self {
//     ListNode {
//       next: None,
//       val
//     }
//   }
// }
impl Solution {
    pub fn merge_k_lists(mut lists: Vec<Option<Box<ListNode>>>) -> Option<Box<ListNode>> {
        let n = lists.len();
        Self::dfs(&mut lists, 0, n)
    }

    fn dfs(
        lists: &mut Vec<Option<Box<ListNode>>>,
        start: usize,
        end: usize,
    ) -> Option<Box<ListNode>> {
        if end - start <= 1 {
            if lists.get(start).is_some() {
                return lists[start].take();
            }
            return None;
        }
        let mid = start + (end - start) / 2;
        let mut left = Self::dfs(lists, start, mid);
        let mut right = Self::dfs(lists, mid, end);
        let mut dummy = Box::new(ListNode::new(0));
        let mut cur = &mut dummy;
        while left.is_some() || right.is_some() {
            let mut next = None;
            if left.is_some()
                && (right.is_none() || left.as_ref().unwrap().val < right.as_ref().unwrap().val)
            {
                let t = left.as_mut().unwrap().next.take();
                next = left.take();
                left = t;
            } else {
                let t = right.as_mut().unwrap().next.take();
                next = right.take();
                right = t;
            }
            cur.next = next;
            cur = cur.next.as_mut().unwrap();
        }
        dummy.next
    }
}

# Definition for singly-linked list.
class ListNode {
    public $val;
    public $next;
    public function __construct($val = 0, $next = null)
    {
        $this->val = $val;
        $this->next = $next;
    }
}

class Solution {
    /**
     * @param ListNode[] $lists
     * @return ListNode
     */

    function mergeKLists($lists) {
        $numLists = count($lists);

        if ($numLists === 0) {
            return null;
        }
        while ($numLists > 1) {
            $mid = intval($numLists / 2);
            for ($i = 0; $i < $mid; $i++) {
                $lists[$i] = $this->mergeTwoLists($lists[$i], $lists[$numLists - $i - 1]);
            }
            $numLists = intval(($numLists + 1) / 2);
        }
        return $lists[0];
    }

    function mergeTwoLists($list1, $list2) {
        $dummy = new ListNode(0);
        $current = $dummy;

        while ($list1 != null && $list2 != null) {
            if ($list1->val <= $list2->val) {
                $current->next = $list1;
                $list1 = $list1->next;
            } else {
                $current->next = $list2;
                $list2 = $list2->next;
            }
            $current = $current->next;
        }
        if ($list1 != null) {
            $current->next = $list1;
        } elseif ($list2 != null) {
            $current->next = $list2;
        }
        return $dummy->next;
    }
}

23 - Merge k Sorted Lists

23 - Merge k Sorted Lists

MergeSort solution

big-o analysis

Heap-Based Solution

Key Implementation Details

Example

Conclusion

All Problems

All Solutions

Welcome to Subscribe On Youtube

23 - Merge k Sorted Lists

MergeSort solution

big-o analysis

Heap-Based Solution

Key Implementation Details

Example

Conclusion

All Problems

All Solutions