There are n unique candies (labeled 1
through n) and k bags. You are asked to distribute
all the candies into the bags such that every bag has at
least one candy.
There can be multiple ways to distribute the candies. Two ways are considered different if the candies in one bag in the first way are not all in the same bag in the second way. The order of the bags and the order of the candies within each bag do not matter.
For example, (1), (2,3) and (2), (1,3) are considered
different because candies 2 and 3 in the bag
(2,3) in the first way are not in the same bag in the second way (they
are split between the bags (2) and (1,3)).
However, (1), (2,3) and (3,2), (1) are considered the same
because the candies in each bag are all in the same bags in both ways.
Given two integers, n and k, return the
number of different ways to distribute the candies. As the
answer may be too large, return it modulo 109 + 7.
Example 1:
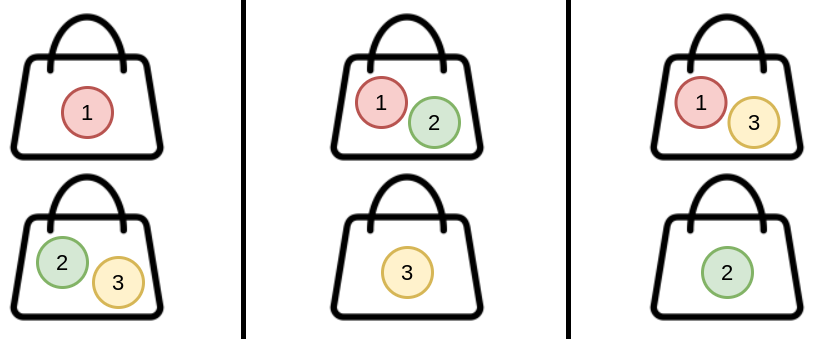
Input: n = 3, k = 2 Output: 3 Explanation: You can distribute 3 candies into 2 bags in 3 ways: (1), (2,3) (1,2), (3) (1,3), (2)
Example 2:
Input: n = 4, k = 2 Output: 6 Explanation: You can distribute 4 candies into 2 bags in 7 ways: (1), (2,3,4) (1,2), (3,4) (1,3), (2,4) (1,4), (2,3) (1,2,3), (4) (1,2,4), (3) (1,3,4), (2)
Example 3:
Input: n = 20, k = 5 Output: 206085257 Explanation: You can distribute 20 candies into 5 bags in 1881780996 ways. 1881780996 modulo 109 + 7 = 206085257.
Constraints:
1 <= k <= n <= 1000