1612. Check If Two Expression Trees are Equivalent

A binary expression tree is a kind of binary tree used to represent arithmetic expressions. Each node of a binary expression tree has either zero or two children. Leaf nodes (nodes with 0 children) correspond to operands (variables), and internal nodes (nodes with two children) correspond to the operators. In this problem, we only consider the '+' operator (i.e. addition).

You are given the roots of two binary expression trees, root1 and root2. Return true if the two binary expression trees are equivalent. Otherwise, return false.

Two binary expression trees are equivalent if they evaluate to the same value regardless of what the variables are set to.

Follow up: What will you change in your solution if the tree also supports the '-' operator (i.e. subtraction)?

Example 1:

Input: root1 = [x], root2 = [x]
Output: true

Example 2:

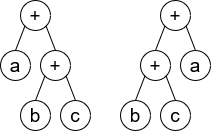
Input: root1 = [+,a,+,null,null,b,c], root2 = [+,+,b,c,a]
Output: true
Explaination: a + (b + c) == (b + c) + a

Example 3:

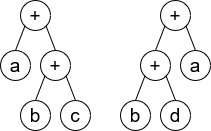
Input: root1 = [+,a,+,null,null,b,c], root2 = [+,+,b,d,a]
Output: false
Explaination: a + (b + c) != (b + d) + a

Constraints:

• The number of nodes in both trees are equal, odd and, in the range [1, 4999].
• Node.val is '+' or a lower-case English letter.
• It's guaranteed that the tree given is a valid binary expression tree.