1557. Minimum Number of Vertices to Reach All Nodes

Given a directed acyclic graph, with n vertices numbered from 0 to n-1, and an array edges where edges[i] = [fromi, toi] represents a directed edge from node fromi to node toi.

Find the smallest set of vertices from which all nodes in the graph are reachable. It's guaranteed that a unique solution exists.

Notice that you can return the vertices in any order.

Example 1:

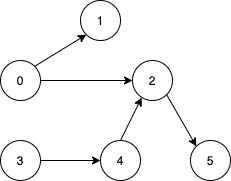
Input: n = 6, edges = [[0,1],[0,2],[2,5],[3,4],[4,2]]
Output: [0,3]
Explanation: It's not possible to reach all the nodes from a single vertex. From 0 we can reach [0,1,2,5]. From 3 we can reach [3,4,2,5]. So we output [0,3].

Example 2:

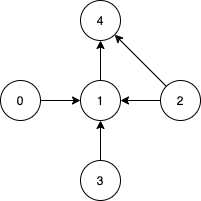
Input: n = 5, edges = [[0,1],[2,1],[3,1],[1,4],[2,4]]
Output: [0,2,3]
Explanation: Notice that vertices 0, 3 and 2 are not reachable from any other node, so we must include them. Also any of these vertices can reach nodes 1 and 4.

Constraints:

• 2 <= n <= 10^5
• 1 <= edges.length <= min(10^5, n * (n - 1) / 2)
• edges[i].length == 2
• 0 <= fromi, toi < n
• All pairs (fromi, toi) are distinct.