1537. Get the Maximum Score

You are given two sorted arrays of distinct integers nums1 and nums2.

A valid path is defined as follows:

• Choose array nums1 or nums2 to traverse (from index-0).
• Traverse the current array from left to right.
• If you are reading any value that is present in nums1 and nums2 you are allowed to change your path to the other array. (Only one repeated value is considered in the valid path).

Score is defined as the sum of uniques values in a valid path.

Return the maximum score you can obtain of all possible valid paths.

Since the answer may be too large, return it modulo 10^9 + 7.

 

Example 1:

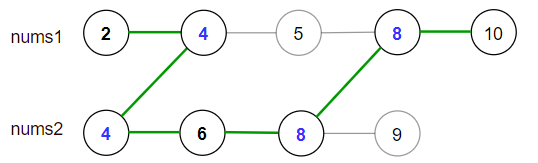
Input: nums1 = [2,4,5,8,10], nums2 = [4,6,8,9]
Output: 30
Explanation: Valid paths:
[2,4,5,8,10], [2,4,5,8,9], [2,4,6,8,9], [2,4,6,8,10],  (starting from nums1)
[4,6,8,9], [4,5,8,10], [4,5,8,9], [4,6,8,10]    (starting from nums2)
The maximum is obtained with the path in green [2,4,6,8,10].

Example 2:

Input: nums1 = [1,3,5,7,9], nums2 = [3,5,100]
Output: 109
Explanation: Maximum sum is obtained with the path [1,3,5,100].

Example 3:

Input: nums1 = [1,2,3,4,5], nums2 = [6,7,8,9,10]
Output: 40
Explanation: There are no common elements between nums1 and nums2.
Maximum sum is obtained with the path [6,7,8,9,10].

Example 4:

Input: nums1 = [1,4,5,8,9,11,19], nums2 = [2,3,4,11,12]
Output: 61

 

Constraints:

• 1 <= nums1.length <= 10^5
• 1 <= nums2.length <= 10^5
• 1 <= nums1[i], nums2[i] <= 10^7
• nums1 and nums2 are strictly increasing.