1135. Connecting Cities With Minimum Cost

There are N cities numbered from 1 to N.

You are given connections, where each connections[i] = [city1, city2, cost] represents the cost to connect city1 and city2 together.  (A connection is bidirectional: connecting city1 and city2 is the same as connecting city2 and city1.)

Return the minimum cost so that for every pair of cities, there exists a path of connections (possibly of length 1) that connects those two cities together.  The cost is the sum of the connection costs used. If the task is impossible, return -1.

Example 1:

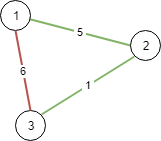
Input: N = 3, connections = [[1,2,5],[1,3,6],[2,3,1]]
Output: 6
Explanation: 
Choosing any 2 edges will connect all cities so we choose the minimum 2.

Example 2:

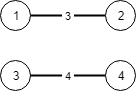
Input: N = 4, connections = [[1,2,3],[3,4,4]]
Output: -1
Explanation: 
There is no way to connect all cities even if all edges are used.

Note:

1. 1 <= N <= 10000
2. 1 <= connections.length <= 10000
3. 1 <= connections[i][0], connections[i][1] <= N
4. 0 <= connections[i][2] <= 10^5
5. connections[i][0] != connections[i][1]