1026. Maximum Difference Between Node and Ancestor

Given the root of a binary tree, find the maximum value V for which there exists different nodes A and B where V = |A.val - B.val| and A is an ancestor of B.

(A node A is an ancestor of B if either: any child of A is equal to B, or any child of A is an ancestor of B.)

Example 1:

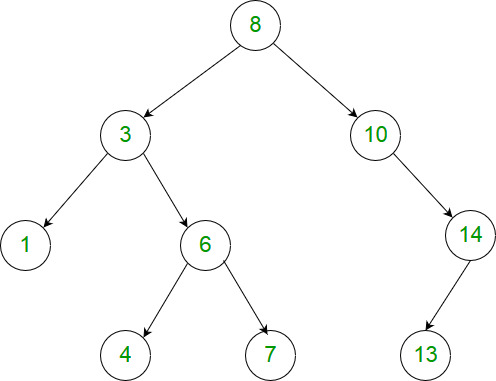
Input: [8,3,10,1,6,null,14,null,null,4,7,13]
Output: 7
Explanation: 
We have various ancestor-node differences, some of which are given below :
|8 - 3| = 5
|3 - 7| = 4
|8 - 1| = 7
|10 - 13| = 3
Among all possible differences, the maximum value of 7 is obtained by |8 - 1| = 7.

Note:

1. The number of nodes in the tree is between 2 and 5000.
2. Each node will have value between 0 and 100000.